在拥堵的车流中走走停停，旁边车道的车却总能呼啸而过，这可能是很多人曾经遇到过的情境。
然而这到底是错觉还是事实，其中是否蕴含科学道理？
是的，这是错觉，不然哪需要我写这么多🙃
其实在1999年，Nature就曾有一篇短篇通讯讨论过这个问题。
作者来自斯坦福大学的HRP(Departments of Health Research and Policy and of Statistics)。
可能是作者研究领域的原因，文中对此交通现象的原理并未从交通学科的角度深度挖掘。
因此本文分别从交通工程学与心理生理学的角度来进行完整的剖析。
交通流理论：陷入拥堵的时间总是更多
试想如下两车道场景，存在长度为$L$的交错交通波，灰色部分（记为区域1）以平均速度$V_{1}$缓慢前进。
灰色部分之间的区域2则以一更快的平均速度$V{2}$前进，即$V{2}>V_1$。
但两类区域均为拥堵状态（区域2并不是自由流）。
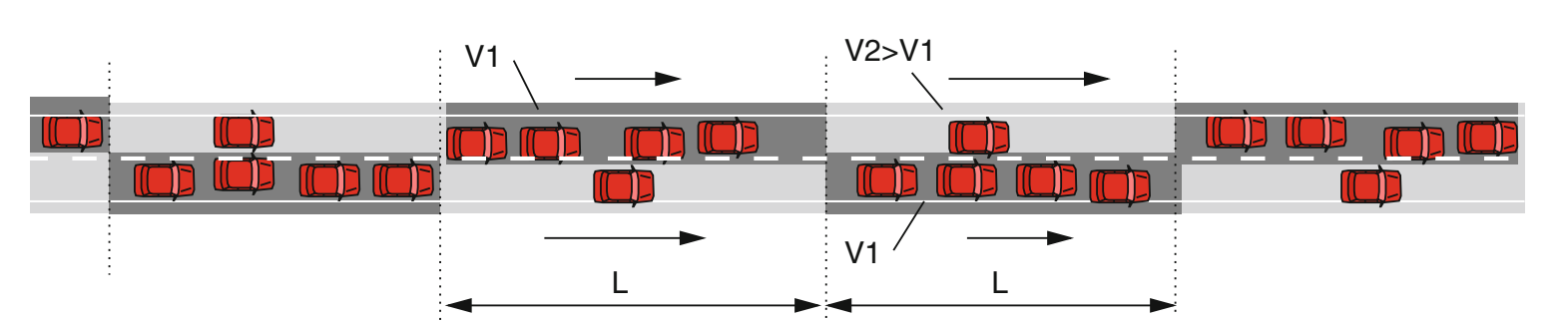
假设此场景的宏观基本图为典型的三角形，且速度调整时间忽略不计（可以认为相应跟驰模型为OVM或是Newell模型）。
因此区域1和区域2分别对应基本图中箭头所示的两点。
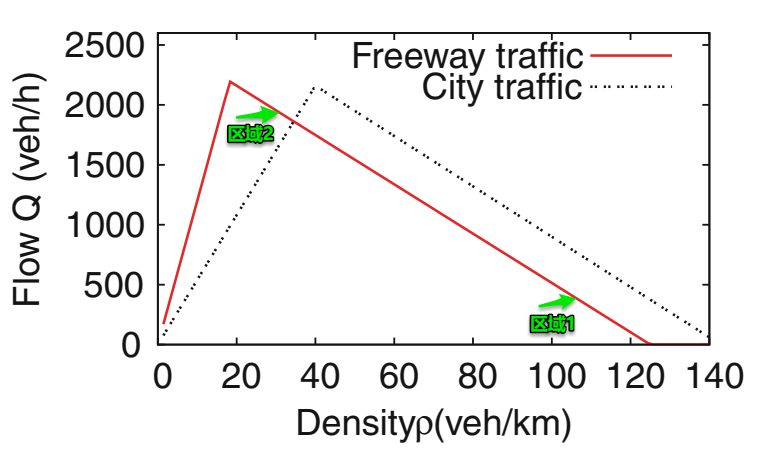
根据交通波理论，从区域1传至区域2的波速$c$为一恒定值，假定为$-5m/s^2$，即图中的两点连线的斜率。 $$ c=\frac{Q_2-Q_1}{\rho_2-\rho_1}=-5m/s^2 $$ 注意到斜率为负数，即此阻塞波的传播方向与车辆行驶方向相反，如下图所示。
因此车辆在区域$1$的相对速度为$V_1+|c|$，相应的于区域$1$中渡过的时间为$\tau_1=\frac{L}{V_1+|c|}$。
同理车辆在区域$2$的相对速度为$V_2+|c|$，相应的于区域$2$中渡过的时间为$\tau_2=\frac{L}{V_2+|c|}$。
同时假定$V_1=0$，$V_2=10m/s^2$，因此整体行程时间中挤在拥堵区域的比例为： $$ \frac{\tau_1}{\tau_1+\tau_2}=\frac{v_2+|c|}{v_1+v_2+2|c|}=\frac{3}{4} $$ > 即对于任意一辆车来说，在整个行程中有超过50%的时间是陷入缓慢的“爬行”中的。
而两条车道的平均速度是相同的，即使换道也会落入该车道的交通波中，最后的行程时间毫无差别。
因此总觉得旁边车道更快是不符合交通流理论的。
心理生理学：视线中的错觉
从生理学的视角来看，人类在驾驶时，视线总是向前的。
所超越的车辆很快会消失在视野中，而超越本车的车辆仍会在视线中留存一段更长的时间。
同时，人们在拥挤交通流中缓慢前行的闲暇时总是会看向相邻车道。
而从心理学的角度来说，人们对于被超越带来的失落感往往大于超车带来的快感。
综上才会认为旁边的车道总是比本车道更快。
正如古语所说，这山望着那山高，“ The Grass is Always Greener on the Other Side”。
Reference
Traffic Flow Dynamics：
http://www.traffic-flow-dynamics.org/#trafficFlowDynamicsPage
Why cars in the next lane seem to go faster：
https://www.nature.com/articles/43360
— 完 —
